Parte I

Ítem 1
Ítem 2
Ítem 3

1. Iremos analisar os seguintes mapas com curvas de nível, obtidas no site web da Faculdade de Engenharia Agrícola - Unicamp

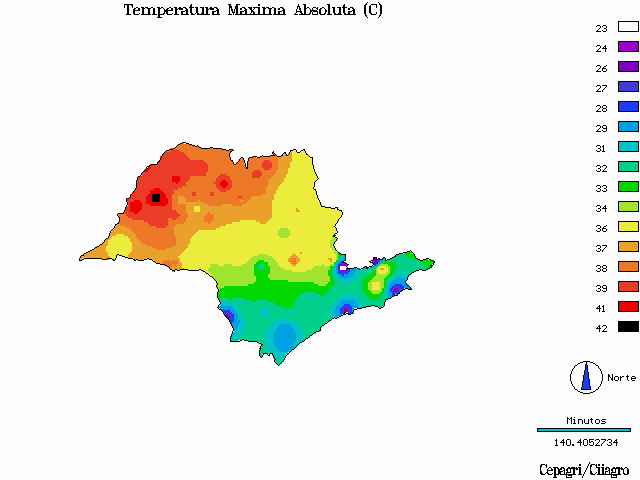
    O mapa acima é uma representação gráfica da temperatura mínima atingida em diversas regiões do estado de São Paulo em um determinado período de tempo. Esta é uma representação bidimensional de um gráfico que poderia ser projetado em três dimensões (longitude, latitude e temperatura). Definindo o eixo z como o eixo da temperatura, teríamos valores maiores nas regiões vermelhas e laranjas do gráfico, e valores menores nas regiões azuis do mapa. As regiões amarelas e verdes representam os valores intermediários. Assim, o gráfico seria mais "alto" na região noroeste do estado, abaixando gradativamente em direção ao litoral, atingindo um mínimo na região de Campos do Jordão, na divisa com o sul do estado de Minas Gerais. O gráfico foi obtido com dados obtidos de estações meteorológicas de vários aeroportos, fazendas, cidades e centros de pesquisas. Assim obtém-se valores para cada área do estado. O mesmo vale para os dois gráficos abaixo:

    Neste caso podemos observar que as temperaturas ainda tendem a ser maiores na região do noroeste paulista, mas agora os mínimos foram atingidos também na região da cidade de São Paulo e também na região de Itapéva e Ribeira, na fronteira com o estado do Paraná.

    Verificamos ainda que as maiores temperaturas estão no oeste do estado. Assim, podemos deduzir que o gasto de energia elétrica com ar condicionado nessa região do estado deve ser maximizada. Felizmente, devido à proximidade de várias usinas hidroelétricas (como Jupiá, Ilha Solteira e Porto Primavera), há uma perda menor de energia pelo efeito Joule (pelos fios). Assim, a natureza otimizou a distribuição de altas temperaturas, colocando-as próximas às fontes de energia elétrica.

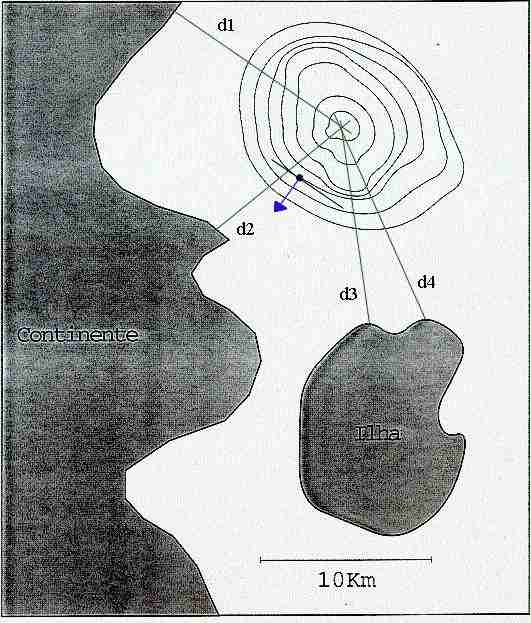
  2. Estudando o mapa anexo (mapa 20), que contém dados sobre um fictício derramamento de óleo perto de um litoral, podemos tirar várias conclusões. Primeiramente, deve-se esclarecer que o mapa é uma representação das dimensões da mancha de óleo em intervalos de 30 minutos. Deduzimos então que se trata de um mapa de curvas de nível, representando a expansão da mancha em função do tempo.

1. Para encontrar a provável localização do navio no instante do derramamento de óleo, traçamos algumas retas partindo do centro das curvas até a última curva de nível (indicadas por d1, d2, d3 e d4). Percebe-se que a reta d1 é a maior das quatro, logo, num determinado intervalo de tempo (3 horas e meia), o óleo expandiu-se mais nessa direção (sua velocidade de expansão é maior). Assim, a provável origem da mancha estará deslocada no sentido contrário de d1 no centro aproximado de todas as curvas de nível. O vetor gradiente no ponto indicado no mapa foi obtido traçando-se uma tangente à curva de nível no ponto dado. O vetor gradiente é perpendicular à essa tangente no sentido de expansão da mancha.
2. Desenhamos quatro retas do centro das curvas de nível até quatro pontos das praias em que a mancha pode chegar primeiro. Foram escolhidos os quatro pontos mais próximos à origem da mancha.

A tabela abaixo expõe os dados que sugeriram a nossa conclusão

A distância D é a distância do centro da mancha até a última curva de nível na direção dada (1, 2, 3 ou 4). A distância d é do centro da mancha até o litoral nessa direção. A velocidade v foi obtida dividindo-se a distância D pelo tempo que a mancha levou para chegar na última curva de nível (3h30). O tempo t representa o tempo que a mancha levará para chegar no litoral, se sua velocidade média na direção dada permanecer a mesma.

Assim concluímos que a mancha chegará no litoral em primeiro no ponto 2.

    3. Vamos utilizar o mapa de temperatura máxima para analisar um caso fictício semelhante ao do ítem dois.

41C - 1.5 litros/hora

42C - 1.75 litros/hora

Para resolver este grave problema, devemos estudar o mapa fornecido. A temperatura de 34C é representada no mapa pela cor verde clara. Para se chegar mais rapidamente a essas regiões, o estudante deve escolher a região mais próxima. Percebemos que há três regiões candidatas: Ourinhos, Botucatu e São Carlos.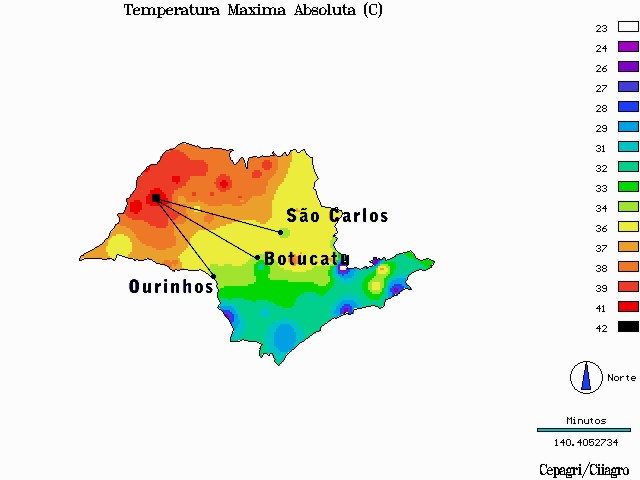

Fazendo-se as medidas no mapa, percebe-se que os 3 caminhos passam por variações de temperatura. Supondo-se que a nave do estudante viaje em linha reta, as distâncias percorridas em cada região de temperatura são (em km):

As distâncias foram calculadas usando a escala 1:12500000

Assumindo-se que a velocidade do disco voador em questão seja constante (de 62.5km/h), sabe-se que ele percorre 12.5km em exatamente 12 minutos (as distâncias foram minimamente ajustadas em múltiplos de 12.5 para facilitar os cálculos)

Utilizando-se os valores dados para a desidratação em função do tempo, temos que a desidratação total em cada caso é:

Indo para São Carlos: 3.94 l

Indo para Botucatu: 3.47 l

Indo para Ourinhos: 3.27 l

Conclui-se então que a solução ótima para o problema do nosso herói é dirigir-se para a cidade de Ourinhos. Se bem que ele também poderia dirigir-se para Botucatu, esta não seria a solução recomendada pois o fator limitante fica muito próximo ao valor crítico (a não ser que ele tenha parentes, amigos ou namorada em Botucatu)!

Como nota post-script deste ítem, gostaríamos de informar que na verdade a melhor opção seria ir até o rio Tietê (a apenas 23km de Andradina), se ele tiver coragem, ou então, utilizando-se de um julgamento mais sábio, dirigir-se ao rio Paraná (a 26km) para se oferecer um banho refrescante.