Parte II
A matemática, além de nos fornecer condições suficientes para prevermos o tempo, estudar o regime de um rio, auxilia no mapeamento topográfico ou ainda ser muito útil para os avançados cálculos de engenharia mecânica. O que nos proporcionou um pequeno devaneio na área aeronáutica.
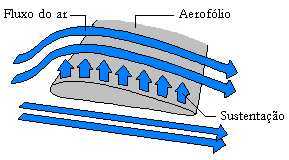
A partir de agora iremos tentar mostrar como o cálculo seria utilizado para otimizar a sustentação de uma asa, de algum avião qualquer. Na figura abaixo, podemos observar as principais forças que agem em um avião
 Para isso, teremos que estudar o teorema de
Bernolli, e entender o que é sustentação e arrasto.
O Teorema de Bernolli
Bernolli foi um ‘cientista’ que além
de estudar cálculo diferencial e integral entre outras coisas, enunciou a lei que diz:
‘quanto maior for o fluxo de ar que passa por uma determinada superfície, menor
será a pressão a que essa estará submetida’.
Para isso, teremos que estudar o teorema de
Bernolli, e entender o que é sustentação e arrasto.
O Teorema de Bernolli
Bernolli foi um ‘cientista’ que além
de estudar cálculo diferencial e integral entre outras coisas, enunciou a lei que diz:
‘quanto maior for o fluxo de ar que passa por uma determinada superfície, menor
será a pressão a que essa estará submetida’.
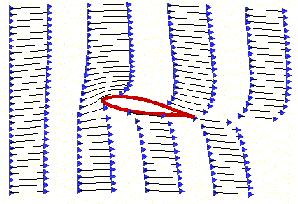
Vejamos os exemplo que ilustra a situação:

Isso ocorre por que o com o ar em movimento sobre a superfície da água, promove a diminuição da pressão que o liquido está submetido. Assim a água tende a ‘voar’.
Esse trabalho elaborado por Bernolli, foi responsável por grande parte da evolução da aeronáutica. Nada mais que promoveu o inicio da realização de um dos sonhos mais antigos do homem, VOAR.
O Arrasto A força conhecida como arrasto é aquela causada pela resistência e pela turbulência do ar.Para melhor ilustrar: quando você estiver andando com seu carro em uma auto estrada, tente colocar a mão para fora da janela. Você irá observar que ela tenderá ficar para trás.
Outro exemplo clássico do efeito da resistência do ar é : em algum dia de ventania, observe um pequeno zunido vido dos fios de alta tensão. Esse barulho se deve ao ar em turbilhonamento.
Puxando o assunto para os aviões, podemos observar que, em seus projetos, tendem a minimizar o arrasto. Pois o intuito é minimizar o turbilhonamento. Vejamos algumas ilustrações:
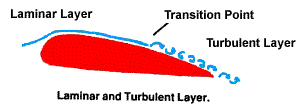
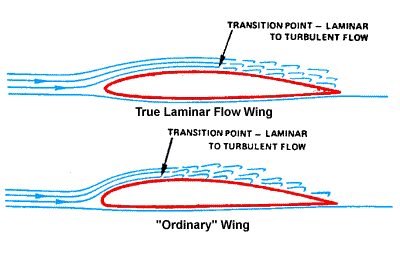
 Para evitar o turbilhonamento do ar na
superfície da asa, adota-se a forma de carenagem arredondada, para que como na figura
acima o turbilhonamento ocorra na parte posterior do aerofólio, isto é, o perfil que
nós conhecemos de asa é esse pois ele ‘força’ o ar a se deslocar sobre a
superfície de forma natural como se essa
estivesse apenas ‘cortando’, procurando manter o ambiente como era antes, sem
turbulência.
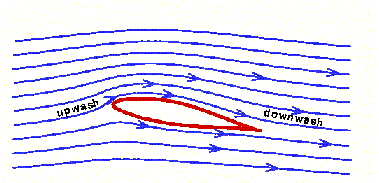
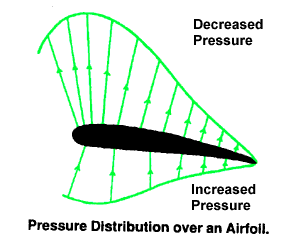
Note que pela figura abaixo, que a velocidade do
ar no extradorso (em cima) é maior que no intradorso (embaixo). Mas a velocidade do ar no
final do aerofólio tende a ser igual se otimizado o arrasto.
Para evitar o turbilhonamento do ar na
superfície da asa, adota-se a forma de carenagem arredondada, para que como na figura
acima o turbilhonamento ocorra na parte posterior do aerofólio, isto é, o perfil que
nós conhecemos de asa é esse pois ele ‘força’ o ar a se deslocar sobre a
superfície de forma natural como se essa
estivesse apenas ‘cortando’, procurando manter o ambiente como era antes, sem
turbulência.
Note que pela figura abaixo, que a velocidade do
ar no extradorso (em cima) é maior que no intradorso (embaixo). Mas a velocidade do ar no
final do aerofólio tende a ser igual se otimizado o arrasto.
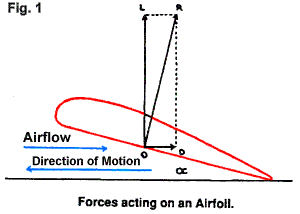
 Nesta figura, podemos entender com mais clareza
quais as forças que agem em uma asa. Note a resultante, a soma vetorial de L
(Sustentação) e D (Arrasto).
Nesta figura, podemos entender com mais clareza
quais as forças que agem em uma asa. Note a resultante, a soma vetorial de L
(Sustentação) e D (Arrasto).
 As figuras abaixo ilustram o que o turbilhonamento
na ponta da asa pode fazer com o ar:
As figuras abaixo ilustram o que o turbilhonamento
na ponta da asa pode fazer com o ar:

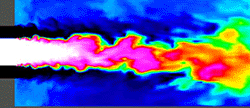
Muitas pessoas sempre acharam que esse desenho feito nas nuvens era devido as turbinas ou ao deslocamento de ar das hélices dos aviões. Mas não, isso ocorre pelo turbilhonamento que ocorre na asa.
Por que otimizar o arrasto (o volume , a sustentação e o bordo de ataque):
As aeronaves são classificadas em:
Na confecção de uma aeronave, leva-se em conta o fim que essa aeronave irá tomar.
Para uma aeronave de transporte, devido seu tamanho o arrasto produzido pelo bordo de ataque é compensado pela sustentação gerada pela asa. Podemos observar que a diferença da distância que o ar percorre no extra pelo intradorso é relativamente grande, pois assim o ar deverá ‘correr’ mais no extra do que no intradorso, pois só assim poderá existir uma diferença de pressão entre a parte superior da asa com a parte inferior, e possíbilitando o vôo. Em alguns casos essa diferença de velocidade chega a 25%.
Quanto maior for a velocidade do ar, maior será o atrito cinético do escoamento sobre a superfície; o que acarreta um aumento de temperatura no aerofólio. Observe os vetores gradientes que indicam a pressão sofrida nesses pontos.
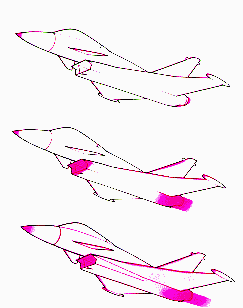 Para os Militares, que por natureza não desejam
ser detectados pelos radares infravermelhos do inimigo, promovem pesquisas que envolvem
milhões de dólares para evitar esses problemas, pois por voarem em situações críticas
isso seria muito prejudicial. Veja o caso abaixo, aeronaves de menor bordo de ataque são
mais difíceis de serem detectadas (como: T-38 e F-16) em relação aos de maiores como o
TU-95. (asdistâncias estão em milhas náuticas/km).
Para os Militares, que por natureza não desejam
ser detectados pelos radares infravermelhos do inimigo, promovem pesquisas que envolvem
milhões de dólares para evitar esses problemas, pois por voarem em situações críticas
isso seria muito prejudicial. Veja o caso abaixo, aeronaves de menor bordo de ataque são
mais difíceis de serem detectadas (como: T-38 e F-16) em relação aos de maiores como o
TU-95. (asdistâncias estão em milhas náuticas/km). 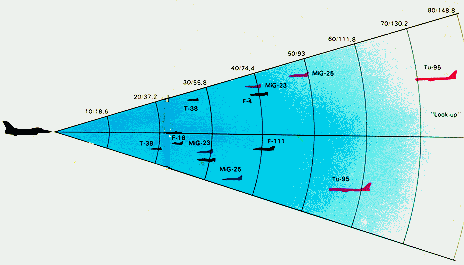 Argumentos que iremos utilizar em nossos cálculos de
otimização:
Argumentos que iremos utilizar em nossos cálculos de
otimização:
Após vários refinamentos matemáticos nas fórmulas que nos permite equacionar a sustentação e o arrasto, temos:
Para a sustentação:
![]()
Para o arrasto causado pela asa:
![]()
onde:
L= sustentação;
Cl = coeficiente de sustentação;
r = densidade do ar;
v= velocidade;
S= Área da seção vertical da asa;
CD= coeficiente de arrasto.
Cálculos
Nosso maior empecílio nesse projeto foi a ausência de apoio computacional que nos auxiliasse na formulação de equações matemáticas que nos desse uma de uma maneira próxima da real , o perfil de um aerofólio.
Uma asa pode ser entendida (analisando os eixos x, y, z) da seguinte maneira:
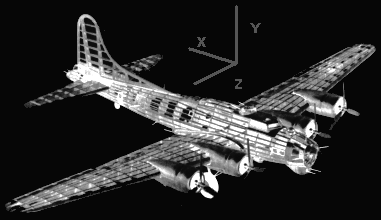
Fazendo-se cortes sucessivos em XY variando Z de 0 (encostado na fuselagem) até a ponta da asa, obtemos as seções:
![]()
![]()
![]()
![]()
Como já discutimos anteriormente, estaremos otimizando uma asa em função do bordo de ataque , sustentação e arrasto. Para tal iremos nos utilizar de uma ou mais equações que nos forneçam o intra e o extradorso.
Para ilustrar o como poderia ser feito a asa desse B-17, usamos o programa Mathematica versão 3.0 e tentamos ser fiéis ao modelo. Veja abaixo, o procedimento usado para desenhar esse aerofólio:
ParametricPlot3D [ {3*r*Cos[t], (1/10)*r*Sin[t], 1+r^2} , {t,0,Pi} ,{r,0,20}]
E encontramos :
Agora o Extra Dorso:
ParametricPlot3D [ {3*r*Cos[t], r*Sin[t], 1+r^2} , {t,Pi,2*Pi} , {r,0,20}
E: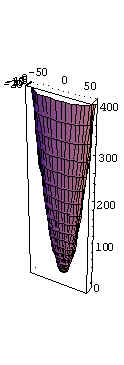
ParametricPlot3D [ {r^2-30, 2*r*Cos[t], 2*r*Sin[t]+250} , {t,0,2*Pi} , {r,0,10};
Motor 2:
ParametricPlot3D [ {r^2-20, 2*r*Cos[t], 2*r*Sin[t]+350} , {t,0,2*Pi} , {r,0,10};
Assim, os motores terão a forma de um parabolóide:
Motor 1: Motor 2: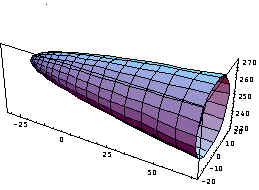
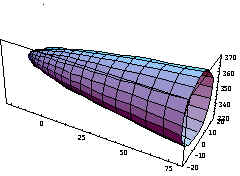
Unindo todos os desenhos em um só, pelo comando ‘Show[a,b,c,d]’, temos:
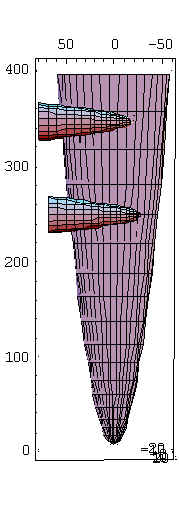
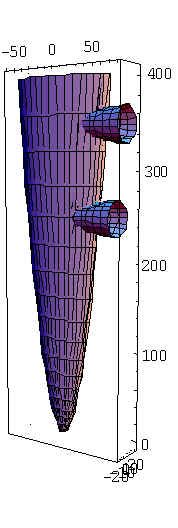 Vista do Intra Dorso Vista do ExtraDorso
Vista do Intra Dorso Vista do ExtraDorso
Nessa asa não conseguimos a perfeição na semelhança do desenho com o real, por vários motivos já discutidos. As principais diferenças são:
Como não nos foi possivel até agora otimizar o funcionamento de uma asa qualquer, escolhemos o Su-26MX (fabricado pela Sukhoi, industria Russa) pelo falto de ter sido o único ao qual tivemos acesso aos perfis NACA.
Para melhores esclarecimentos: Esse avião é um modelo acrobático, que pode voar a baixas velocidades sem perder sustentação (isso é, uma de suas caracteristicas é a baixa velocidade de stol) para efetuar suas manobras. Ele já é um modelo ótimo, portanto faremos o contrário ao que foi sugerido (iremos desotimizá-lo).
Obs.: Se a agência Russa demorou quase 20 anos para otimizar com eficiência reconhecida e imitada até os dias de hoje, não seremos nós, alunos calouros e novatos na área (apesar de muito interessados nela) , que em dois meses iríamos otimizá-lo e derrubá-los do pódium. Nós não queremos inventar a roda!
O alvo da ‘desotimização’, eis o mito, Su-26MX:
 O que é NACA?
O que é NACA?
Nada mais é do que uma norma técnica que dá as características do perfil (eixo xy) do aerofólio.
No nosso caso, o perfil de NACA 0010 é dado pelos pontos:
| Upper x | Upper y | Lower x | Lower y |
| 0 | 0 | 0 | 0 |
| .25 | .7 | .25 | -.7 |
| .5 | .95 | .5 | -.95 |
| 1 | 1.4 | 1 | -1.4 |
| 1.25 | 1.60 | 1.25 | -1.58 |
| 2.5 | 2.20 | 2.5 | -2.18 |
| 5 | 2.98 | 5 | -2.96 |
| 7.5 | 3.51 | 7.5 | -3.5 |
| 10 | 3.95 | 10 | -3.9 |
| 15 | 4.47 | 15 | -4.46 |
| 20 | 4.78 | 20 | -4.78 |
| 25 | 4.95 | 25 | -4.95 |
| 30 | 5 | 30 | -5 |
| 40 | 4.84 | 40 | -4.84 |
| 50 | 4.41 | 50 | -4.41 |
| 60 | 3.8 | 60 | -3.8 |
| 70 | 3.05 | 70 | -3.05 |
| 80 | 2.19 | 80 | 2.19 |
| 90 | 1.21 | 90 | -1.21 |
| 100 | .11 | 100 | -.11 |
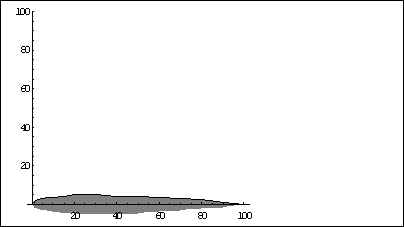
Pelo programa Mathematica, podemos através do comando ‘Fit’ descobrir qual a função de cada curva ( a do extra e intradorso), são elas:
E = 0.0000606824276334679701 + 1.63756860254691138* x0.605326876513317202 - 0.263699191260363052*x
I = 0.0096719243581745502 - 1.64625045045784741* x0.6100128126906650436 + 0.271086647497547561*x
Veja como seria o perfil desse NACA:
 A partir de agora, todos os cálculos
estarão sujeitos a um fator de correção para a escala real S=0,018 .Iniciamos agora com
o cálculo do comprimento do extra e intradorso pela formula:
A partir de agora, todos os cálculos
estarão sujeitos a um fator de correção para a escala real S=0,018 .Iniciamos agora com
o cálculo do comprimento do extra e intradorso pela formula:
![]()
Assim para o extradorso temos: Comprimento extra = 1.82567m;
E para o intra: Comprimento intra = 1.82538m.
Analogamente, para o NACA 23012:
Os pontos:
| Upper x | Upper y | Lower x | Lower y |
| 0 | 0 | 0 | 0 |
| .2 | .65 | .2 | -.55 |
| .5 | 1.55 | .5 | -.85 |
| 1 | 2.3 | 1 | -1.15 |
| 1.25 | 2.67 | 1.25 | -1.23 |
| 2.5 | 3.61 | 2.5 | -1.71 |
| 5 | 4.91 | 5 | -2.26 |
| 7.5 | 5.8 | 7.5 | -2.61 |
| 10 | 6.43 | 10 | -2.92 |
| 15 | 7.19 | 15 | -3.5 |
| 20 | 7.5 | 20 | -3.97 |
| 25 | 7.6 | 25 | -4.28 |
| 30 | 7.55 | 30 | -4.46 |
| 40 | 7.14 | 40 | -4.48 |
| 50 | 6.41 | 50 | -4.17 |
| 60 | 5.47 | 60 | -3.67 |
| 70 | 4.36 | 70 | -3 |
| 80 | 3.08 | 80 | -2.16 |
| 90 | 1.68 | 90 | -1.23 |
| 95 | .92 | 95 | -.70 |
| 100 | .13 | 100 | -.13 |
E = 0.000568442138250302431 + 2.66218306475660515* x0.581223009456498385 – 0.386397298071799255*x
I = 0.000926293765223591742 – 1.33146805501421972* x0.712514606549434237 + 0.354463051698646758*x
Assim o perfil será:
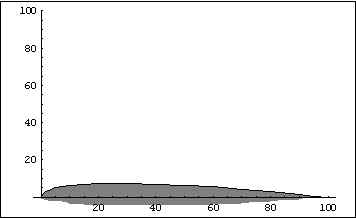 Comprimento do extra e intra dorso:
Comprimento do extra e intra dorso:
Comprimento extra = 1.85559 m;
Comprimento intra = 1.81777 m.
Calculando a velocidade mínima (Stol):
Como nessa situação o peso deve ser igual a força de sustentação, temos:![]()
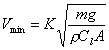
![]()
ve = 101.5702 km/h (54.844 nós);
Pressão dinâmica: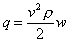
[q] = Pa = N/m²;
w = 9.94
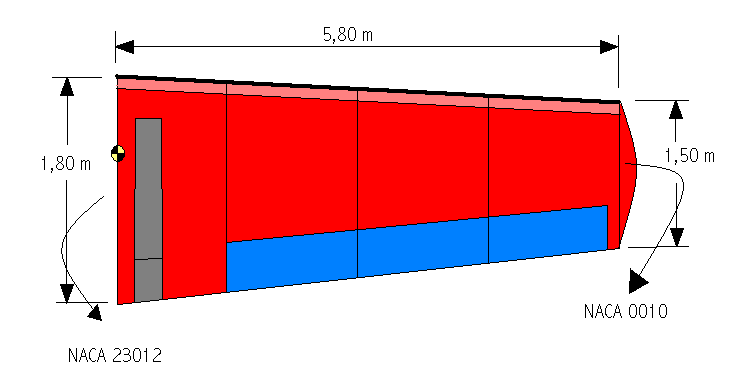
A Sustentação é dada por: L = Cl A (qe – qi ) [L] = NComo a projeção horizontal do Sukhoi é:
Como o NACA não é constante nas nervuras, iremos usar um artifício matemático para calcular o seu volume:
![]()
Onde :
b é comprimento da asa;
a = 0 (zero);
Ba : Bordo de ataque (y = 1.8 + 0.0175 x);
Bf : Bordo de fuga ( y = 0.0349 x);
Assim:
V = 0.970104 m³ (970.104 litros)
Para otimizarmos esse aerofólio, precisamos do arrasto. Como já mostrado:![]()
E no NACA 0010, os pontos são: para o extra (30,5) e no intra (30,-5), com amplitude de 10.
Desse modo a área da vista frontal ( que tem a forma de um trapésio de lado maio = 12.01*0.018 , e lado menor = 10*0.018 e altura de 5.8 m) é 1.1489 m².
Pelo diagrama abaixo, podemos deduzir que:
 Sendo:
Sendo:
tg a = L / D
assim:
![]()
Se tg a for menor que o definido para essa asa, o avião não irá voar, pois isso significa que o peso está igual a força de sustentação, isso é , está na iminência de começar a cair.
Para essa asa, que tem os NACAs variando iremos calcular a média aritmética dos coeficientes de sustentação (Cl) e dos coeficientes de arrasto (Cd).
Então se a for menor que 86.5649o a aeronave não conseguirá voar!!!
Agora vamos ver algumas variações das equações que foi aproximada para os NACAs que possuímos:
Ampliação para 1.2 do original os NACAs:
NACA 23012
E = (0.000568442138250302431 + 2.66218306475660515* x0.581223009456498385 – 0.386397298071799255*x)*1.2
I = (0.000926293765223591742 – 1.33146805501421972* x0.712514606549434237 + 0.354463051698646758*x)*1.2
Podemos observar no gráfico abaixo, a curva original (em verde) e a desotimizada (em vermelho):
 NACA 0010:
NACA 0010:
E = (0.0000606824276334679701 + 1.63756860254691138* x0.605326876513317202 – 0.263699191260363052*x)*1.2
I = (0.0096719243581745502 - 1.64625045045784741* x0.6100128126906650436 + 0.271086647497547561*x)*1.2
No grafico abaixo, podemos observar como no anterior, curva original (em verde) e desotimizada ( em vermelho):

A = 1.3653 m²
Assim a ![]() será 85.9202,
portanto a asa em questão, deixa de cumprir seu papel na medida que não consegue mais
sustentar esse avião para aquela velocidade de Stol.
será 85.9202,
portanto a asa em questão, deixa de cumprir seu papel na medida que não consegue mais
sustentar esse avião para aquela velocidade de Stol.
Até agora você viu e esperamos que tenha entendido como é feito os perfil de aerofólios. Só não mostramos mais por alguns motivos relevantes como:
A falta de um aparato computacional mais eficiente e por não temos conhecimentos muito aprofundados na área de aeronáutica, apesar de sermos apaixonados por tudo que se diz voar! A escolha de tentar otimizar uma asa de um avião qualquer, surgiu pela liberdade que tivemos para escolher o assunto, e além disso pela vontade de descobrir como as coisas funcionam!
Todos nós, que estávamos envolvidos pelo projeto, ralamos muito, mas muito mesmo, estudamos, pesquisamos, ligamos para empresas que trabalham na área, procuramos professores (da FEM e do IMECC) além de consultar amigos, amigos dos amigos e vizinhos dos cunhados do pai da namorada do primo do dono do bar da esquina que serviu uma cerveja pro bisneto do Santos Dumont, que trabalham ou irão trabalhar com aeronaútica ou mecânica.
Nesta parte do projeto, apesar de não termos tido sucesso em realmente otimizar uma asa, aprendemos muito sobre engenharia aeronáutica (ainda não podemos nos considerar experts na tecnologia do vôo, mas saímos desse projeto com uma visão diferente sobre esse assunto) e aplicações diretas da matemática na engenharia, por isso, consideramos que para nós este projeto foi um enorme sucesso.
Essa liberdade de escolher como queremos aprender um determinado assunto, como Cálculo, nos promoveu a união do útil ao agradável. Aprendemos fazendo o que gostamos.
